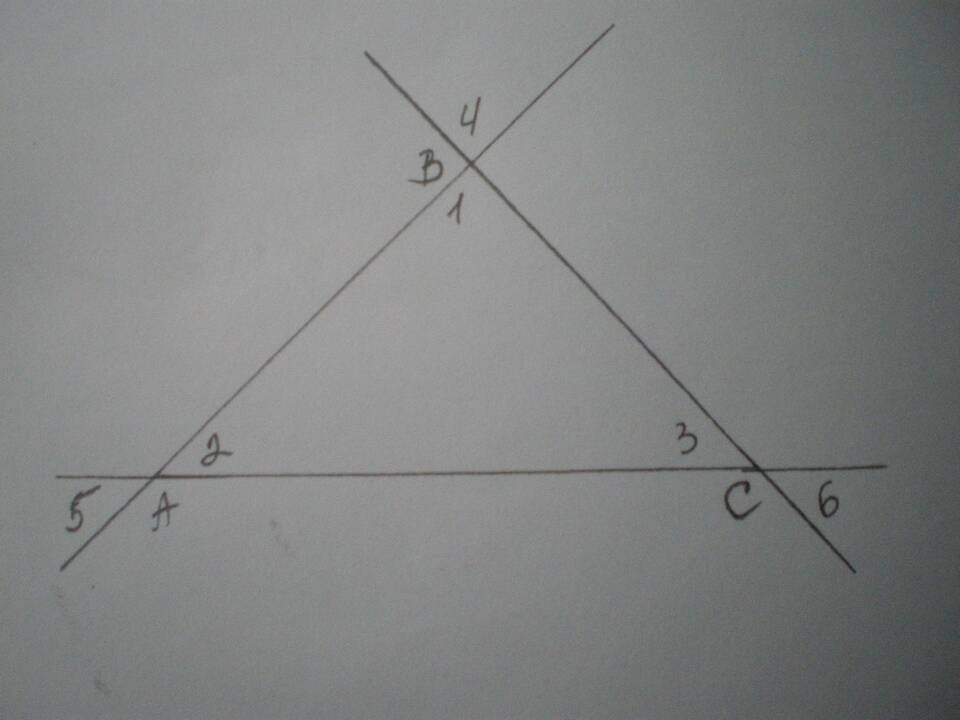
В геометрии сумма внешних углов треугольника является важной характеристикой этой фигуры. Внешний угол треугольника образуется при продолжении одной из его сторон и смежен с внутренним углом фигуры.
Содержание
В геометрии сумма внешних углов треугольника является важной характеристикой этой фигуры. Внешний угол треугольника образуется при продолжении одной из его сторон и смежен с внутренним углом фигуры.
Основная теорема о сумме внешних углов
Сумма внешних углов треугольника, взятых по одному при каждой вершине, всегда равна 360 градусов. Это утверждение справедливо для любого треугольника, независимо от его вида (остроугольного, прямоугольного или тупоугольного).
Доказательство теоремы
- В любом треугольнике сумма внутренних углов равна 180°
- Каждый внешний угол является смежным с внутренним и в сумме с ним дает 180°
- Для трех вершин имеем: (180° - A) + (180° - B) + (180° - C)
- Преобразуем выражение: 540° - (A + B + C) = 540° - 180° = 360°
Свойства внешних углов
| Свойство | Описание |
| Величина внешнего угла | Равна сумме двух внутренних углов, не смежных с ним |
| Количество внешних углов | У треугольника ровно три внешних угла |
| Зависимость от типа треугольника | Сумма всегда 360° независимо от вида треугольника |
Пример расчета
Рассмотрим треугольник с внутренними углами 60°, 70° и 50°:
- Первый внешний угол: 180° - 60° = 120°
- Второй внешний угол: 180° - 70° = 110°
- Третий внешний угол: 180° - 50° = 130°
- Сумма внешних углов: 120° + 110° + 130° = 360°
Данное свойство треугольников широко применяется в геометрии, архитектуре и инженерных расчетах. Понимание этой закономерности помогает решать различные задачи, связанные с треугольными конструкциями и их измерениями.
