Доверительный интервал позволяет оценить диапазон значений, в котором с определенной вероятностью находится истинный параметр генеральной совокупности. Рассмотрим методы расчета границ доверительного интервала для различных статистических параметров.
Содержание
Основные понятия
| Термин | Определение |
| Доверительный уровень | Вероятность, с которой интервал содержит истинный параметр (обычно 90%, 95% или 99%) |
| Стандартная ошибка | Мера изменчивости выборочной статистики |
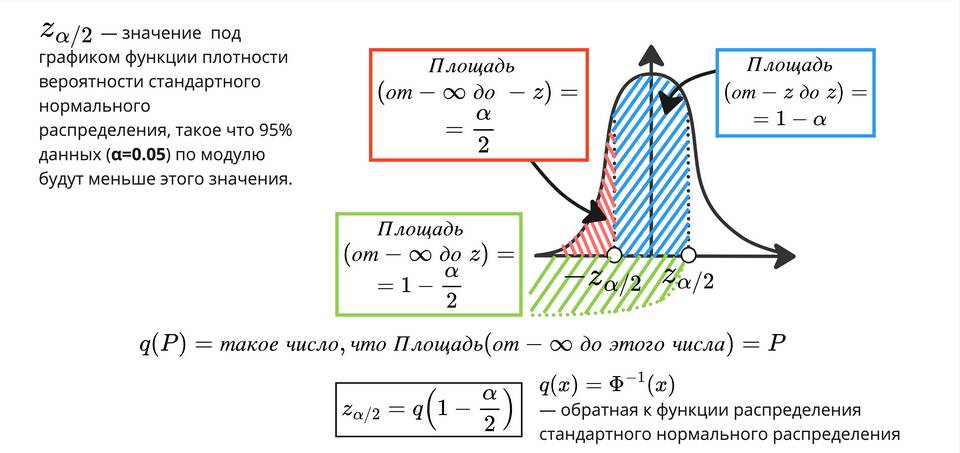
| Критическое значение | Z- или t-значение, соответствующее выбранному доверительному уровню |
Формула общего вида
Доверительный интервал = Точечная оценка ± (Критическое значение × Стандартная ошибка)
Расчет для среднего значения
При известном σ (стандартном отклонении генеральной совокупности)
- Нижняя граница = x̄ - zα/2 × (σ/√n)
- Верхняя граница = x̄ + zα/2 × (σ/√n)
При неизвестном σ (используется t-распределение)
- Нижняя граница = x̄ - tα/2,n-1 × (s/√n)
- Верхняя граница = x̄ + tα/2,n-1 × (s/√n)
Критические значения для разных доверительных уровней
| Доверительный уровень | Z-значение | t-значение (n=30) |
| 90% | 1.645 | 1.699 |
| 95% | 1.960 | 2.045 |
| 99% | 2.576 | 2.756 |
Расчет для доли признака
Формула Вальда:
- Нижняя граница = p̂ - zα/2 × √(p̂(1-p̂)/n)
- Верхняя граница = p̂ + zα/2 × √(p̂(1-p̂)/n)
Пошаговый алгоритм расчета
- Определите точечную оценку параметра (среднее, доля)
- Выберите доверительный уровень (обычно 95%)
- Найдите соответствующее критическое значение
- Рассчитайте стандартную ошибку
- Вычислите границы интервала
- Интерпретируйте результаты
Пример расчета для среднего
| Параметр | Значение |
| Выборочное среднее (x̄) | 50 |
| Стандартное отклонение (s) | 10 |
| Объем выборки (n) | 100 |
| 95% доверительный интервал | 50 ± 1.96 × (10/√100) = [48.04, 51.96] |
Важные замечания
- Для малых выборок (n < 30) используйте t-распределение
- При анализе долей убедитесь, что np̂ > 5 и n(1-p̂) > 5
- Ширина интервала зависит от объема выборки и изменчивости данных
- Доверительный интервал не означает вероятность для конкретного параметра