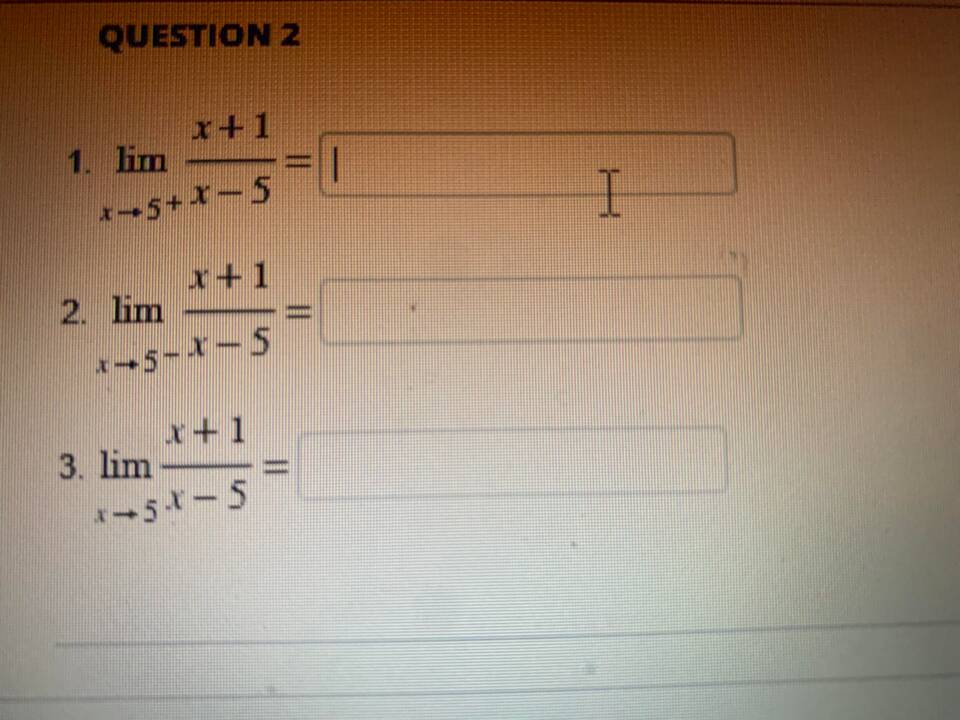
Понятие лимита (предела) является фундаментальным в математическом анализе и описывает поведение функции при приближении аргумента к некоторой точке. Это ключевое понятие лежит в основе дифференциального и интегрального исчисления.
Содержание
Основное определение предела
| Термин | Определение |
| Предел функции | Число, к которому стремится значение функции при приближении аргумента к заданной точке |
| Обозначение | limx→a f(x) = L |
Виды пределов
По типу стремления аргумента
- Конечный предел при x→a
- Предел на бесконечности (x→∞)
- Односторонние пределы (слева и справа)
По характеру результата
- Конечный предел
- Бесконечный предел
- Несуществующий предел
Основные свойства пределов
| Свойство | Формулировка |
| Единственность | Функция не может иметь два разных предела в одной точке |
| Локальная ограниченность | Если предел существует, функция ограничена в окрестности точки |
| Арифметические свойства | Предел суммы, разности, произведения и частного |
Вычисление пределов: основные методы
- Непосредственная подстановка
- Разложение на множители
- Умножение на сопряженное выражение
- Использование замечательных пределов
- Правило Лопиталя
Примеры вычисления пределов
Рассмотрим несколько типичных случаев:
- limx→2 (3x + 1) = 7 (непосредственная подстановка)
- limx→0 (sin x)/x = 1 (первый замечательный предел)
- limx→∞ (1 + 1/x)x = e (второй замечательный предел)
Понятие предела является краеугольным камнем современной математики и находит применение не только в анализе, но и в других разделах математики, физике, инженерии и экономике. Понимание пределов необходимо для изучения производных, интегралов и рядов.